Paradoxe de Monty Hall, simulation R
Une simulation statistique R du célèbre jeu télévisé américain Let's Make a Deal.
"Let's Make a Deal", le célèbre jeu télévisé américain présenté par Monty Hall était diffusé, dans sa version originale, de 1963 à 1977. 35 ans plus tard, son adaptation française a donné naissance au "Bigdil" présenté par Vincent Lagaf'. Un grand moment de télévision...
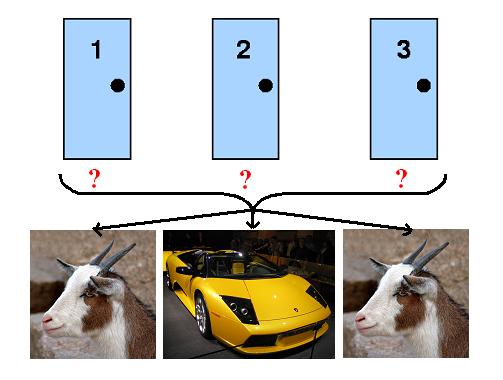
Voici le principe du jeu:
Simulation avec R:
Pour simuler le choix d'une porte avec R, on peut par exemple utiliser la fonction replicate:
choix=c(0,1,0)
Ntirages=1000
tirages=replicate(Ntirages,sample(1:3,1))
On garde ainsi en mémoire les choix initiaux.
En moyenne le gain de la voiture est donc:
mean(choix[tirages])
0.326
Phase 2 du jeu:
tirages2=tirages
changement=c()
for(i in 1:Ntirages)
{
# choix restant
tirage=c(1:3)[-tirages[i]]
# le présentateur élimine 1 des 2 mauvaises portes
tirage=tirage[-which(tirage %in% c(1,3))[1]]
# le candidat décide ou non de changer son choix
change=sample(0:1,1)
if(change==1) tirages2[i]=tirage
# on sauvegarde les changements de choix
changement=c(changement,change)
}
On obtient ainsi la probabilité de gagner par groupe (ceux qui ont changé d'avis et ceux qui n'en ont pas changé).
res.df=data.frame(changement=changement,gain=choix[tirages2])
mapReduce(map=changement,moyenne=mean(gain),data=res.df)
moyenne
0 0.316
1 0.663
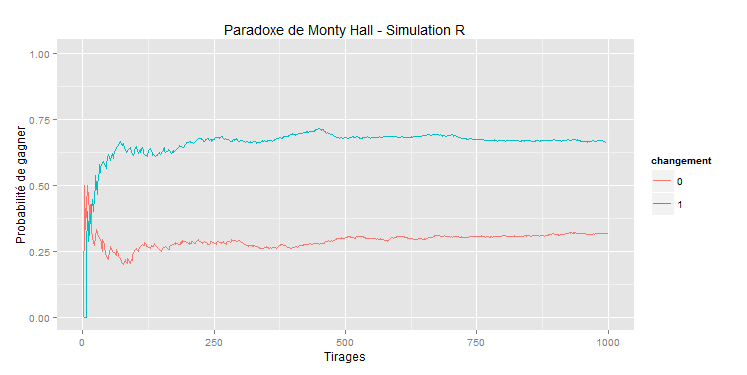
Convergence de l'estimateur
Conclusion:
Il n'y a que les imbéciles qui ne changent pas d'avis.
Source photo et introduction: fr.wikipedia.org/wiki/Probl%C3%A8me_de_Monty_Hall
Voici le principe du jeu:
- 3 portes
- 2 chèvres
- 1 voiture

Quelle porte choisissez-vous?
So, let's make a deal:
Vous avez, a priori, 1 chance sur 3 de trouver la voiture. C'est alors que le présentateur du jeu ouvre une des portes ne cachant pas la voiture. Il vous fait ensuite une nouvelle proposition:
- Conservez-vous votre choix initial?
- Voulez-vous changer de porte?
Alors, quelle est la meilleure stratégie?
Solution théorique:
La solution théorique est bien connue et s'exprime à l'aide du théorème de Bayes: 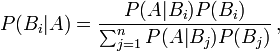
Imaginons que le candidat ait choisi la porte numéro 3 pour commencer. Le présentateur ouvre la porte numéro 1. Le candidat doit-il modifier son choix initial?
On trouve ainsi, sur la page Wikipédia du paradoxe de Monty Hall, le résultat concernant la possibilité que la voiture soit derrière la porte 2 sachant que le présentateur ouvre la porte 1 : 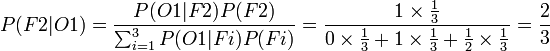
Simulation avec R:
Pour simuler le choix d'une porte avec R, on peut par exemple utiliser la fonction replicate:
choix=c(0,1,0)
Ntirages=1000
tirages=replicate(Ntirages,sample(1:3,1))
On garde ainsi en mémoire les choix initiaux.
En moyenne le gain de la voiture est donc:
mean(choix[tirages])
0.326
Phase 2 du jeu:
tirages2=tirages
changement=c()
for(i in 1:Ntirages)
{
# choix restant
tirage=c(1:3)[-tirages[i]]
# le présentateur élimine 1 des 2 mauvaises portes
tirage=tirage[-which(tirage %in% c(1,3))[1]]
# le candidat décide ou non de changer son choix
change=sample(0:1,1)
if(change==1) tirages2[i]=tirage
# on sauvegarde les changements de choix
changement=c(changement,change)
}
On obtient ainsi la probabilité de gagner par groupe (ceux qui ont changé d'avis et ceux qui n'en ont pas changé).
res.df=data.frame(changement=changement,gain=choix[tirages2])
mapReduce(map=changement,moyenne=mean(gain),data=res.df)
moyenne
0 0.316
1 0.663

Convergence de l'estimateur
Conclusion:
Il n'y a que les imbéciles qui ne changent pas d'avis.
Source photo et introduction: fr.wikipedia.org/wiki/Probl%C3%A8me_de_Monty_Hall
Publié par olivier le 16 novembre 2012.
Lire les commentaires sur paradoxe de monty hall, simulation r