Tests de rangs - Travail d'Etude et de Recherche
Le bûcheron et le géomètre
Un bûcheron doit abattre 12 arbres. Accompagné de son ami le géomètre, il lui demande d'estimer la hauteur des 12 arbres avant de les faire tomber. Celle-ci est calculée par une mesure trigonométrique.
Une fois abattus, ces mêmes arbres sont mesurés au sol. Cette seconde mesure est évidemment précise et considérée comme juste.
La mesure trigonométrique effectuée par le géomètre était-elle bonne ?
Testons 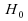 « Il n'y a pas de différences entre les deux
mesures » contre
« Il n'y a pas de différences entre les deux
mesures » contre 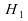 « il y a une différence significative ».
« il y a une différence significative ».
Le
seuil de signification est fixé à 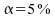 .
.
 Mesures trigonométriques : 20.4, 25.4, 25.6, 25.6, 26.6, 28.6, 28.7, 29, 29.8, 30.5, 30.9, 31.1
Mesures trigonométriques : 20.4, 25.4, 25.6, 25.6, 26.6, 28.6, 28.7, 29, 29.8, 30.5, 30.9, 31.1
Mesures effectuées au sol : 20.7, 26.3, 26.8, 28.1, 26.2, 27.3, 29.5, 32, 30.9, 32.3, 32.3, 31.7
Différences entre les mesures : -0.3, -0.9, -1.2, -2.5, 0.4, 1.3, -0.8, -3.0, -1.1, -1.8, -1.4, -0.6
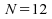 (nombre de différences non nulles)
(nombre de différences non nulles)
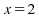 (nombre de différences pour le signe le moins
fréquent).
(nombre de différences pour le signe le moins
fréquent).
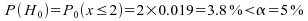 .
.
La
probabilité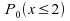 est
donnée par la table des valeurs critiques du test binomial
(nous ne pouvons pas utiliser les quantiles sur une fonction de test
de loi discrète); on multiplie par 2 car le test est
bilatéral.
est
donnée par la table des valeurs critiques du test binomial
(nous ne pouvons pas utiliser les quantiles sur une fonction de test
de loi discrète); on multiplie par 2 car le test est
bilatéral.
Conclusion
: Au niveau 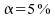 ,
nous concluons à
,
nous concluons à 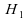 .
Les deux méthodes de mesures ne donnent pas les mêmes
résultats.
.
Les deux méthodes de mesures ne donnent pas les mêmes
résultats.
Approximation normale
Lorsque
N > 25 (N grand), on peut utiliser l'approximation normale, en
faisant intervenir une correction de continuité. Il suffit de
calculer la valeur 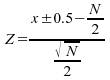 ;
;
où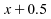 est
utilisé lorsque
est
utilisé lorsque 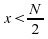 ,
et
,
et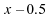 lorsque
lorsque 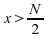 .
.
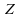 suit
alors une loi normale centrée réduite
suit
alors une loi normale centrée réduite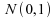 ,
dont nous pouvons déterminer le quantile d'ordre
,
dont nous pouvons déterminer le quantile d'ordre 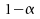 (ou
(ou 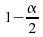 si
le test est bilatéral).
si
le test est bilatéral).
Dans
le cas de l'exemple précèdent,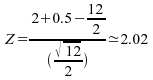 ;
nous obtenons donc
;
nous obtenons donc 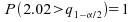 ;
avec
;
avec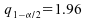 au
niveau
au
niveau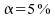 .
.
Bien
que les échantillons ne comportent que 12 individus chacun,
l'approximation est très satisfaisante :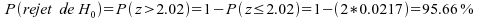 .
.
Nous
concluons également à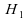 .
.