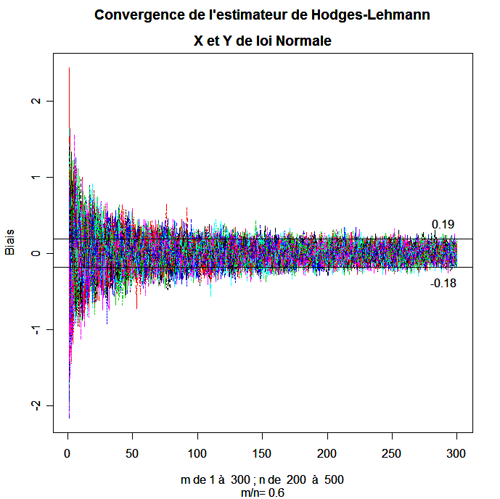
Tests de rangs - Travail d'Etude et de Recherche
Estimateur de Hodges – Lehmann
Le
modèle de localisation est fonction du paramètre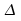
,
paramètre sur lequel repose entièrement le test de la
médiane : il est donc intéressant de chercher à
l'estimer; ce qui est possible grâce à la statistique
.
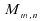Le
principe de cette estimation, dûe à Hodge-Lehmann, est
de translater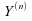
de
,
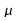de façon à ce que
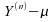soit
le plus proche possible de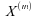
;
proximité évaluée par.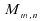
C'est
ce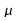qui
va servir dans l'estimation de: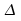
en effet, dans le cas où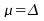
,
on aurait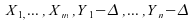
un
échantillon de la même loi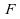
.
Soit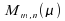
la
loi de: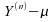
Théorême :
.
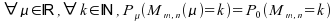Estimation
de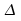par
:
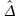1°
On calcule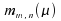
,
telle que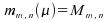
pour
les échantillons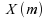
et
;
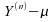2°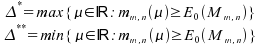
3°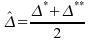
.
Propriétés :
-
-
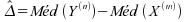
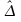est
sans biais
