Tests de rangs - Travail d'Etude et de Recherche
Intervalle de confiance
Il
est possible de déterminer un intervalle de confiance de
niveau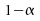
pour
:
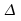Théorème :
Soit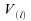
la
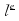statistique
d'ordre de l'ensemble des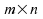
variables
aléatoires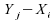
(
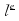valeur
de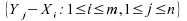
ordonné
croissant);
Soit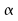
tel
qu'il existe un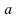
vérifiant
;
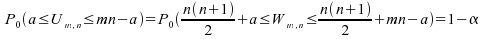Alors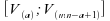
est
un intervalle de confiance de niveau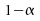pour
.
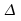Pour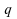
quantile
de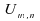
,
on prend pour intervalle de confiance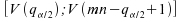
.
b) Approximation normale
Si
l'on connaît ou que l'on dispose de la fonction quantile de,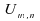
ces intervalles sont faciles à former; mais si ils sont
inconnus, on peut avoir recours à la convergence de la loi
vers une normale :
Pour
retrouver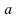correspondant
au seuil,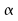
il faut disposer de la fonction quantile de la loi de Umn centrée
:
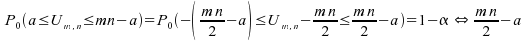est
le quantile d'ordre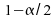
pour
la loi de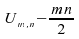
(loi
centrée symétrique).
On
utilise alors la convergence de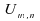centrée
réduite vers la loi normale, pour obtenir des quantiles
approchés.
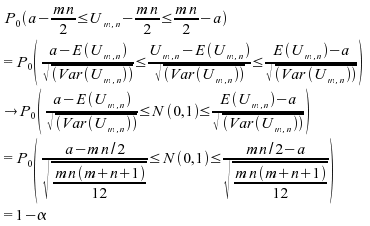
On
obtient donc, asymptotiquement,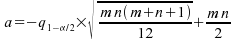
,
avec
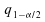quantile
de la loi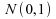
.
c) Application : Test utilisant l'estimateur de Hodges-Lehmann
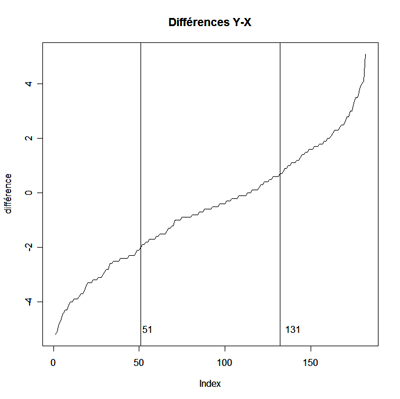
Reprenons l'exemple précèdent sur la hauteur médiane de deux forêts :
Soit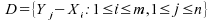
La
statistique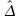
est
égale à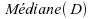
.
Nous
obtenons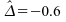
.
On
pose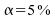
:
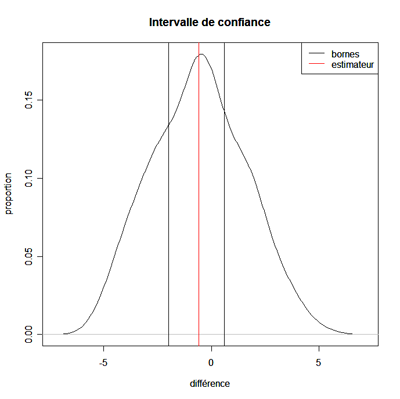
L'intervalle
de confiance au niveau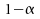
est
;
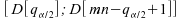avec pour quantile de la loi de Mann-Withney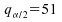
;
soit l'intervalle
.
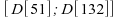Finalement,
l'intervalle de confiance au niveau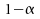de
l'estimateur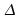
est
donc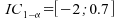 
:
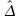appartient
bien à cet intervalle.
d) Application : Approximation normale
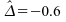
Pour
obtenir l'intervalle de confiance à l'aide de l'approximation
normale nous avons vu qu'il faut calculer :;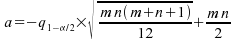
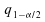avecquantile
de la loi normale.
Nous
avons donc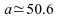
,
;
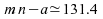en prenant les parties entières, on obtient comme bornes de
l'intervalle de confiance les statistique d'ordre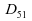
et
;
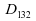soit exactement les mêmes bornes que sans approximation.
Nous
obtenons donc le même intervalle de confiance au niveau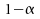de
l'estimateur de :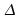
.
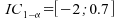L'approximation normale offre donc un résultat très satisfaisant.