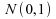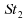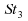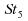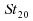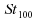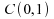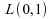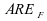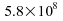Tests de rangs - Travail d'Etude et de Recherche

21 / 11 / 2024
Mention légale
Statisticien.fr

Statistiques d'ordre

a) définitions
Pour un échantillon 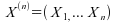donné, à valeurs réelles, d'une loi de probabilité P : on appelle statistique d'ordre le vecteur 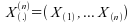de ses valeurs ordonnées croissantes.

Exemple :

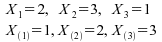
Pour assurer une bijection entre x et sa statistique d'ordre, il faut que toutes les valeurs de x soient bien distinctes; cette condition peut en fait être assurée par la continuité de la fonction de répartition F de la loi P.

 

Théorème : 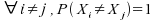si et seulement si F est continue.

Afin d'éviter les problèmes dûs à des échantillons de loi discrètes, de valeurs non toutes distinctes, nous nous limiterons donc au cas des échantillons de loi continue dans toute la suite de l'étude.

Il existe néanmoins, pour certains tests, des méthodes pour contourner l'obstacle des valeurs non distinctes, qui seront évoquées.

Il est possible de déterminer la loi des statistiques d'ordre.

 

Théorème : la fonction de répartition de la statistique d'ordre est donnée par :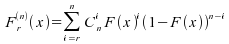

De plus, si F admet une densité f, alors :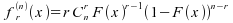

Cette loi, bien que précisément définie, est peu pratique à manipuler et exploiter; il existe toutefois une forme de convergence en loi.

b) convergence en loi

Théorème :

Soit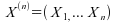un échantillon de loi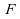, de densité;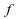

Soit;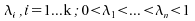

Soit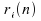la partie entière de;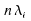

Soit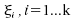les quantiles d'ordr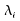e de 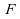; supposons ;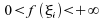

Alors :

Pour ;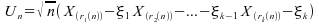

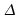matrice symétrique de termes ;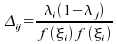

On a 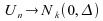en loi.

Dans le cadre de la dimension 1, cette convergence se réduit à

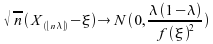, où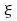est le quantile d'ordr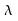e de ;

 

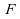Formule que l'on peut encore exprimer, plus directement :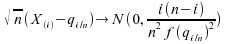. Ainsi, quel que soit l'ordre d'une observation dans un échantillon, cette observation a une convergence en loi vers une loi normale.

Ce théorème permet d'établir une convergence similaire à celle induite par le théorème central limite, mais avec la médiane et non la moyenne :

Soit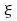la médiane et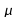l'espérance de la loi;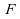

Soit: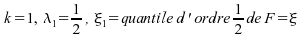

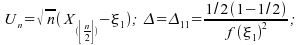
Nous avons donc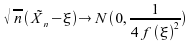; et le TCL :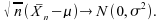

Or, dans le cas d'une loi symétrique,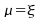(il y a exactement autant de valeurs inférieures à la moyenne que supérieures); donc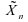 et 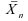estiment le même paramètre.

La question se pose alors de savoir lequel de ces deux estimateurs est le « meilleur », en terme de variance. En fait, il apparaît que selon la loi, le meilleur n'est pas toujours le même.

 

Par exemple, pour la loi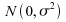, 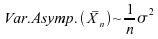et

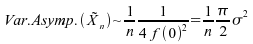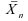: est donc meilleur estimateur que;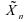

Pour la loi double-exponentielle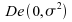, en revanche, 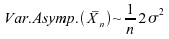et

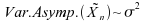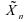: dans ce cas, c'estle meilleur estimateur de la moyenne et médiane.

 

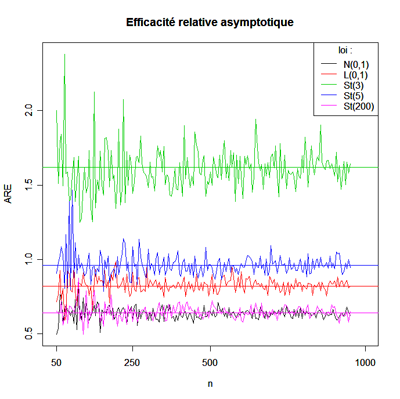
Pour mieux illustrer la comparaison entre les deux estimateurs, considèrons l'Efficacité Relative Asymptotique :

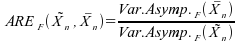
En simulant un grand nombre d'échantillons d'une loi donnée, nous pouvons calculer les ARE de différentes lois. Le tableau suivant a été calculé pour: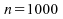

Loi F
	0.63	6.38	1.71	0.98	0.65	0.65		0.8

Ainsi, par exemple, dans les cas de lois de Student à très faible degrés de liberté (3, 4 ou 5), la médiane empirique est un meilleur estimateur que la moyenne empirique.

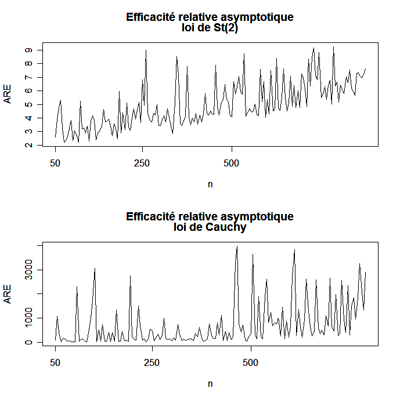
Notons que les ARE des lois de Student à 2 ddl et de Cauchy ne convergent pas; en effet, la loi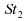n'a pas de variance, et la loi de Cauchy n'a pas de moment d'ordre 1.