Tests de rangs - Travail d'Etude et de Recherche
Statistiques de rangs
La statistique de rang représente tout simplement le rang d'une observation, sa place dans l'échantillon une fois ordonné.
On
nomme rang l'entier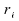
défini
par la relation 
;
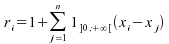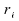est
le rang de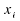
dans
l'échantillon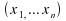
.
Les
valeurs de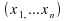
étant
supposées distinctes, le rang constitue une permutation
bijective de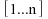 
:
.
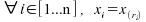Exemple
:
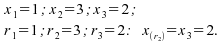
Nous
pouvons ainsi définir la statistique de rangs :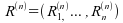 
,
vecteur aléatoire donné par la relation suivante :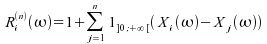 
.
De
la même façon que précédémment,
nous avons donc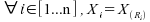 
presque
sûrement.
Il est possible de définir la loi du rang; en fait, c'est tout simplement la loi uniforme; ce qui est cohérent avec l'intuition que l'on a : les probabilités que telle ou telle observation soient d'un certain rang sont réparties de façon égale.
Théorème :
1)
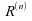suit
une loi uniforme sur l'ensemble des permutations de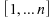
.
2)
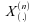et
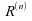sont
indépendantes.
Corollaire :
1)
;
;
.
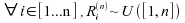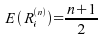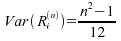2) 
; 
;
.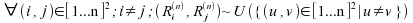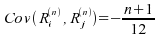
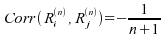