Tests de rangs - Travail d'Etude et de Recherche
Application du test de la médiane (Mood test, 1950)
Le test de la médiane de Mood est un test analogue aux tests d'égalité des moyennes pour des échantillons indépendants. Il a pour principe de déterminer la médiane de l'ensemble des observations, et de dénombrer pour chacun des deux échantillons les observations inférieures et les observations supérieures à cette médiane.
On
peut alors effectuer le test de la médiane, en comparant le
nombre y des observations de l'échantillon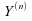
supérieures
à la médiane de l'ensemble, au nombre renvoyé
par la fonction quantile de la loi hypergéométrique.
Nous pourrons également effectuer un test du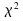
et
comparer le résultat obtenu avec celui du test de Mood.
Les observations initiales sont donc subdivisées en deux catégories par rapport à la médiane générale.
Exemple des forêts
Dans deux types de forêts distincts, nous mesurons les hauteurs respectivement de 13 et 14 peuplements, choisis au hasard et indépendamment, dans le but de vérifier si les hauteurs médianes des deux types de forêts sont ou ne sont pas égales.
Le
niveau du test est fixé à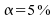
.
Voici les hauteurs des deux peuplements en mètres:
Forêt 1 |
23 .4 |
24.4 |
24.6 |
24.9 |
25 |
26.2 |
26.3 |
26.8 |
26.8 |
26.9 |
27 |
27.6 |
27.7 |
|
Forêt 2 |
22.5 |
22.9 |
23.7 |
24 |
24.4 |
24.5 |
25.3 |
26 |
26.2 |
26.4 |
26.7 |
26.9 |
27.4 |
28.5 |
La médiane générale est M = 26.2, et N = 13 + 14 = 27.
Soit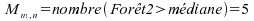
;
or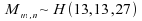
:
:
,
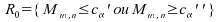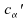quantile d'ordre
,
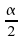vaut 10;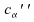 
,
quantile d'ordre
,
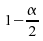vaut 4.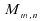
n'est
donc pas dans la région de rejet.
Nous
concluons donc à l'hypothèse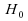
au
seuil: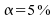
« les forêts ont la même hauteur ».
A titre de comparaison, effectuons
le test du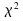sur
ce même exemple :
Les nombres d'observations inférieures et supérieures ou égales à la médiane générale sont donnés dans le tableau suivant :
-
Forêt 1
Forêt 2
Total
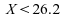
5
8
13
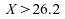
7
5
12
Total
12
13
N = 25
Nous
voulons vérifier que les observations de la réunion des
2 échantillons ont une médiane nulle, c'est à
dire une chance sur deux d'être en-dessous ou au-dessus de la
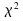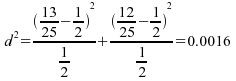
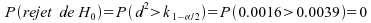médiane. Nous calculons alors la distance du:
,
où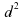
suit
un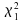
,
et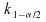
est
le quantile d'ordre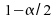
de
la loi.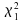
En conclusion, nous pouvons dire que les deux forêts ont une hauteur médiane identique.
Les deux tests ont donné sur cet exemple un résultat identique.
Comparaison entre le test de la médiane et de la moyenne
Prenons le cas d'échantillons gaussiens centrés et de variances égales. Soit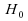l'hypothèse nulle : "Les moyennes des deux échantillons sont les mêmes. " Le
niveau des tests est fixé à.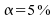
Nous effectuons 400 tests de la médiane et de la moyenne et comparons le pourcentage de rejet de l'hypothèse nulle donné par ces deux tests (test bilatéral):
Résultat :
Le test de la moyenne renvoie un pourcentage de rejet de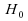d'environ 5%, ce qui était attendu.
Le test de la médiane nous donne un pourcentage également voisin de 5%.
La médiane et la moyenne d'une variable aléatoire qui suit une loi symétrique sont égales. Nous pouvons donc penser que le test de la médiane, pour des variables aléatoires suivant une loi symétrique, est comparable au test de la moyenne.