Tests de rangs - Travail d'Etude et de Recherche
Tests sur deux échantillons indépendants
Les
statistiques de rangs trouvent leur application dans le cadre de
tests de loi entre deux échantillons; c'est à dire,
pour deux échantillons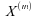 et
et
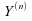 ,
de variable
,
de variable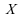 et
et
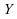 ,
de loi
,
de loi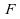 et
et
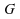 inconnues,
le test
inconnues,
le test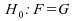 contre
contre
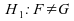 .
.
Plus particulièrement, on s'intéressera ici au modèle dit de localisation :
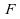 de
médiane nulle (
de
médiane nulle (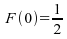 ),
),
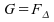 i.e.
i.e.
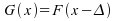 .
.
Nous
effectuerons donc des tests sous l'hypothèse nulle :
«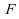 et
et
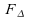 égales
».
égales
».
Le
test de localisation tire son nom du fait qu'il s'agit de déterminer
si les médianes des deux lois sont « localisées »
au même point. Pour ce faire, nous testerons si, après
la réunion des échantillons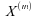 et
et
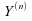 ,
la médiane de la loi
,
la médiane de la loi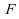 a
été translatée ou non.
a
été translatée ou non.
Ceci
peut être résumé au fait de tester uniquement le
paramètre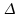 ainsi,
le test d'hypothèse devient
ainsi,
le test d'hypothèse devient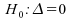 contre
contre
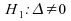 .
.
Bien
les tests se basent alors sur le paramètre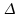 ,
le domaine de statistique reste non paramétrique, car les
lois
,
le domaine de statistique reste non paramétrique, car les
lois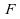 et
et
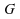 sont
supposées inconnues.
sont
supposées inconnues.
Test de la médiane
Le
principe de ce test est de déterminer la médiane
empirique de la réunion des deux échantillons, et de
compter le nombre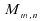 de
termes du second échantillon supérieurs à cette
médiane.
de
termes du second échantillon supérieurs à cette
médiane.
Statistique du test de la médiane :
Soient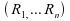 les
rangs de
les
rangs de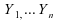 dans
dans
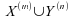 ;
;
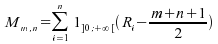 .
.
Sous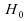 ,
,
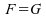 donc
donc
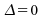 :
donc
:
donc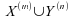 est
un échantillon de loi
est
un échantillon de loi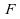 ;
la loi de
;
la loi de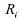 en
est donc indépendante (voir théorème), et
en
est donc indépendante (voir théorème), et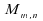 suit
ainsi une loi indépendante de
suit
ainsi une loi indépendante de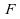 .
.
Théorème
: au niveau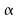 ,
,
-
Cas
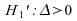 :
:
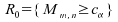 ;
;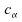 quantile
d'ordre
quantile
d'ordre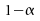 de
de
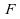 ;
; -
Cas
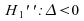 :
:
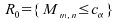 ;
;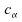 quantile
d'ordre
quantile
d'ordre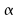 de
de
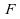 ;
; -
Cas
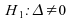 :
:
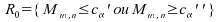 ;
;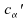 quantile
d'ordre
quantile
d'ordre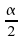 de
de
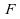 ,
,
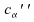 quantile
d'ordre
quantile
d'ordre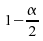 de
de
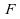 .
.
Théorème :
Sous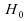 ,
,
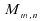 loi
hypergéométrique, de paramètres dépendant
de
loi
hypergéométrique, de paramètres dépendant
de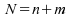 :
:
-
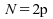 :
: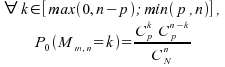
-
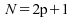 :
: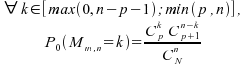
i.e
: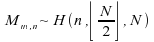 .
.
Corollaire
: sous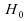 ,
,
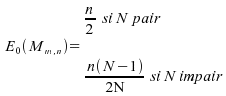
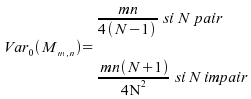
Corollaire
: sous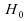 ,
,
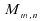 centrée
réduite converge en loi vers la loi gaussienne.
centrée
réduite converge en loi vers la loi gaussienne.
Plus
exactement : si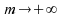 ,
,
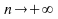 ,
,
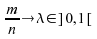 ;
;
alors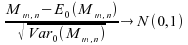 en
loi.
en
loi.
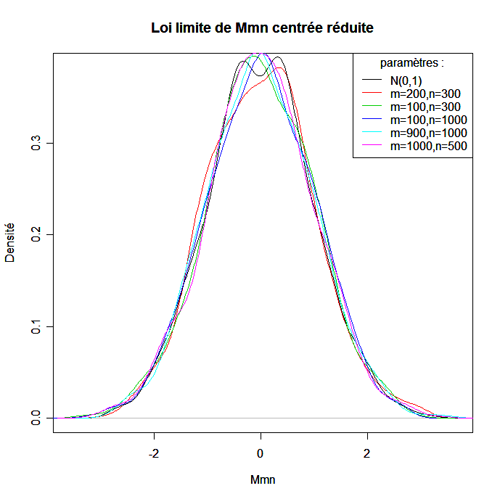
Dans
la pratique, on observe que la convergence s'applique même
pour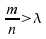 ,
si
,
si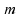 et
et
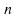 sont
assez grands (la loi hypergéométrique converge vers une
loi binomiale, qui elle même converge vers une loi normale).
sont
assez grands (la loi hypergéométrique converge vers une
loi binomiale, qui elle même converge vers une loi normale).