Tests de rangs - Travail d'Etude et de Recherche
Test de Wilcoxon
Le test des signes n'utilise que l'information sur la direction des différences entre paires. Si nous pouvons prendre en compte, en plus, la grandeur des différences, un test plus puissant peut être utilisé.
Le test de Wilcoxon donne plus de poids à une paire qui montre une large différence entre les deux conditions, qu'à une paire ayant une faible différence. Cela implique que l'on puisse dire quel membre d'une paire est plus grand que l'autre (donner le signe de la différence), mais aussi que l'on puisse ranger les différences en ordre croissant.
Soient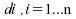 
les
différences entre chaque paire d'observations. Comme pour le
test du signe, nous classons les rangs des valeurs absolues de ces
différences. Mais dans ce cas, la statistique de Wilcoxon
tient compte des rangs des observations.
La statistique de rangs
signés de Wilcoxon s'écrit :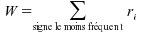
Le test de Wilcoxon peut être complémentaire du test du signe :
Par exemple, si deux
traitements A et B sont équivalents, donc si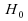
est
vraie, la somme des rangs ayant un signe positif et celle des rangs
ayant un signe négatif devraient être à peu près
égales.
Mais si la somme des rangs de signes positifs est très différente de celle des rangs de signes négatifs, nous en déduirons que le traitement A diffère du traitement B, et rejetterons l'hypothèse nulle.
Dans le cas d'un différence nulle entre deux observations, nous ne tenons pas compte de celles-ci et réduisons en conséquence la taille de l'échantillon.
Si les rangs obtenus contiennent des ex-aequo, nous utiliserons la méthode des rangs moyens :
Par exemple, trois des
paires observées présentent les différences
suivantes :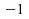
,
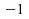et
.
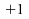Chaque paire aura le rang 2, car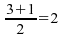
.
La différence suivante aura alors le rang 4, puisque les rangs
1, 2, et 3 ont déjà été utilisés.
Dans
le cas des « grands » échantillons,
lorsque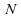
est
supérieur à 25, il peut être démontré
que la somme des rangs
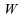est
pratiquement normale; on utilise alors l'approximation normale :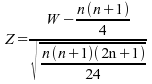 
;
.
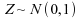