Tests de rangs - Travail d'Etude et de Recherche
Tests de Mann-Whitney et Wilcoxon
Toujours dans le cadre du modèle de localisation, on trouve deux dérivées de l'idée du test de la médiane :
-
Le test de Wilcoxon additionne les rangs des
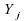 dans
la réunion des échantillons;
dans
la réunion des échantillons; - Le
test de Mann-Whitney compte le nombre de couples pour lesquels
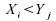 .
.
Ces nombres sont définis ainsi
-
Statistique du test de Wilcoxon :
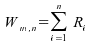 ;
c'est la somme des rangs des termes
;
c'est la somme des rangs des termes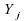 dans
la réunion de
dans
la réunion de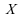 et
et
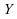 .
.
Pour
une valeur de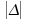 grande,
grande,
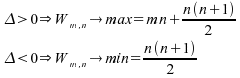
-
Statistique du test de Mann-Whitney :
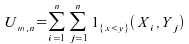 ;
c'est le nombre de termes
;
c'est le nombre de termes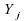 supérieurs
à la médiane de
supérieurs
à la médiane de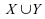 .
.
Pour
une valeur de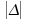 grande,
grande,
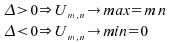
Une relation entre les deux statistiques apparaît :
Théorème
: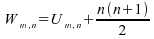
Théorème
: test de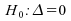 contre
contre
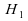 au
niveau
au
niveau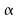 :
:
1)
Cas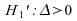 :
:
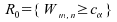 ;
;
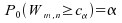
2)
Cas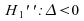 :
:
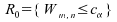 ;
;
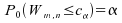
3)
Cas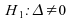 :
:
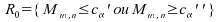 ;
;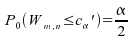 ,
,
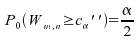
Il
est possible de déterminer les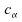 ,
car la statistique
,
car la statistique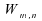 suit
une loi indépendante de F.
suit
une loi indépendante de F.
Elle
se déduit de la loi de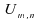 ,
que l'on peut déterminer facilement par récurrence.
,
que l'on peut déterminer facilement par récurrence.
Théorème
: loi de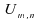 :
:
soit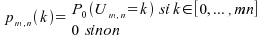 ,
,
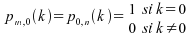 ;
;
alors
: 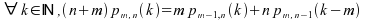 .
.
Corollaire
: sous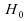 ,
,
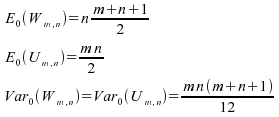
Corollaire
: Si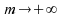 ,
,
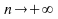 ,
,
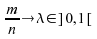 ,
alors :
,
alors :
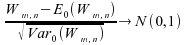 et
et
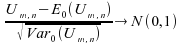 en
loi.
en
loi.
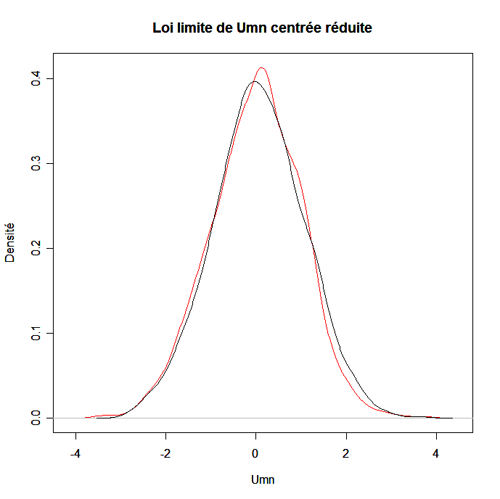
Exemple des forêts avec le test de Mann-Whitney et Wilcoxon

Dans deux types de forêts distincts, nous mesurons les hauteurs respectivement de 13 et 14 peuplements, choisis au hasard et indépendamment, dans le but de vérifier si les hauteurs médianes des deux types de forêts sont ou ne sont pas égales.
Le
niveau du test est fixé à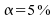 .
.
Voici les hauteurs des deux peuplements en mètres:
Forêt 1 |
23 .4 |
24.4 |
24.6 |
24.9 |
25 |
26.2 |
26.3 |
26.8 |
26.8 |
26.9 |
27 |
27.6 |
27.7 |
|
Forêt 2 |
22.5 |
22.9 |
23.7 |
24 |
24.4 |
24.5 |
25.3 |
26 |
26.2 |
26.4 |
26.7 |
26.9 |
27.4 |
28.5 |
La statistique de Mann-Whitney nous donne U = 71.5. Nous comparons à la valeur renvoyée par la fonction quantile de R pour une probabilité de 97.5%. Nous obtenons q = 131.
Probabilité ( U > q) = 0.
Nous concluons donc à l'hypothèse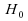 au
seuil
au
seuil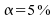 : "Les forêts ont une hauteur médiane identique ".
: "Les forêts ont une hauteur médiane identique ".